Hvordan beregne avstanden til horisonten

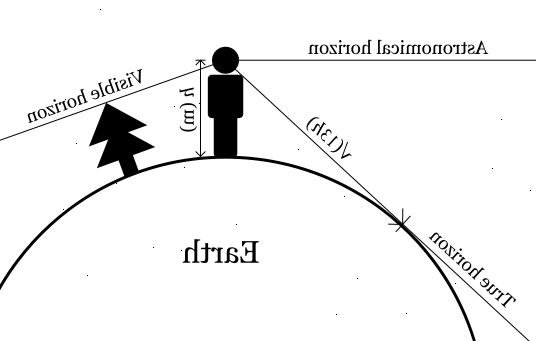
1. 1
   Måle "høyden på øyet." Mål lengden mellom bakken og dine i meter eller fot. En måte å beregne dette på er å måle avstanden mellom din og toppen av hodet. Trekk denne verdien fra din totale høyde og hva som vil være igjen er avstanden mellom øynene og overflaten du står på. Hvis du står nøyaktig på havet, med undersiden av føttene nivå med vannet, er dette den eneste målingen du trenger.
2. 2
   Legg til din "lokal heving" hvis du står på en hevet overflate, for eksempel en ås, bygning eller båt. Hvor mange meter eller fot over den sanne horisonten står du? 1 meter? 4000 fot? Legg dette nummeret til din høyde på øyet (i de samme enhetene, selvfølgelig).
3. 3
   Multipliser med 13m hvis du tok måling i meter, eller multipliser med 1.5ft hvis du tok måling i føttene.
4. 4
   Ta kvadratroten for å finne svaret. Hvis du brukte meter, vil svaret være i kilometer, og hvis føtter, vil svaret være i miles. Reiseavstanden beregnes er en rett linje fra øynene til horisonten. Hvor langt du vil reise for å komme til horisonten vil være lenger på grunn av overflate kurvatur og (på land) uregelmessigheter. Fortsett til neste metoden nedenfor for en mer nøyaktig (og komplisert) formel.
5. 5
   Forstå hvordan denne beregningen fungerer. Det er basert på en trekant dannet av din observasjon punkt (øynene), den sanne horisonten punkt (det du ser på) og sentrum av jorden. Ved å kjenne radius av jorden og måle høyden på øyet og lokal heving, etterlater det bare avstanden mellom øynene og horisonten som ukjent. Siden sidene i trekanten som møtes på horisonten faktisk danner en rett vinkel, kan vi bruke Pythagoras 'læresetning (gode gamle a ^ 2 + b ^ 2 = c ^ 2) som grunnlag for beregningen, hvor:
   • A = R (radius av Jorden)
   • b = avstanden til horisonten, ukjent
   • c = h (din høyde på øyet) + R

Alternativ metode # 1

1. 1
   Beregn den faktiske avstanden du må krysse for å komme til horisonten ved hjelp av denne formelen:
   d = R * arccos (R / (R + h))
   d = avstanden til horisonten
   h = høyde på øyet
   
2. 2
   Øk R med 20% for å kompensere for den forvrenge brytning av lyset stråler og komme fram til en mer nøyaktig måling. Den geometriske horisont beregnet ved hjelp av metoden i denne artikkelen kan ikke være det samme som den optiske horisont, som er det øynene faktisk ser. Atmosfæren bøyer (refracts) lys som er på reise horisontalt. Hva dette betyr vanligvis at en stråle av lys er i stand til lett å følge krumningen på jorden, slik at den optiske horisonten er litt lenger unna enn det geometriske horisonten. Dessverre refraksjon som følge av atmosfæren er hverken konstant eller forutsigbar, siden den er avhengig av endring i temperatur med høyden. Det er derfor ingen enkel måte å legge en korreksjon til formelen for den geometriske horisonten, selv om man kan oppnå en "gjennomsnittlig" korreksjon ved å forutsette en radius på jorden som er litt større enn den sanne radius.
3. 3
   Finne ut hvordan denne beregningen fungerer. Dette vil beregne lengden av den buede linjen som følger av føttene til den sanne horisonten (vist i grønt i dette bildet). Nå, refererer arccos (R / (R + h)) porsjon til den vinkel som er gjort i midten av jorden ved at en linje som går fra den sanne horisont til midten og linjen som går fra dere til midten. Med denne vinkelen, multipliserer vi det ved R for å få "lysbuelengden", som i dette tilfellet, er avstanden som du leter etter.
   

Alternativ metode # 2

1. 1
   Anta en flat fly eller havet. Denne metoden er en enklere versjon av det første sett med instruksjoner som er presentert i denne artikkelen, og rekker bare fot og miles.
2. 2
   Løs for avstanden i miles ved å plugge inn din høyde i øyet i fot (h) inn følgende formel:
   d = 1,2246 * SQRT (h)
   
3. 3
   Utlede formelen fra Pythagoras 'læresetning.
   (R + h) ^ 2 = R ^ 2 + d ^ 2
   Løse for h (. Gjør den forutsetning at R >> h og uttrykke radien av jorden i miles, ca 3959) gir uttrykket:
   d = SQRT (2 * R * h)